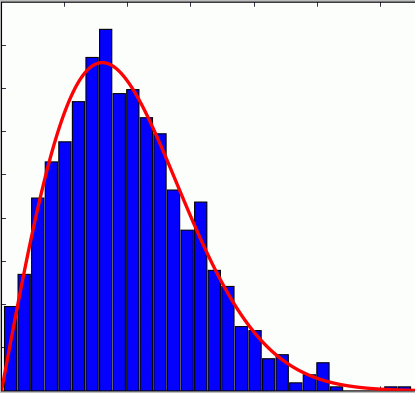
One of the most active and unusual applications of ensembles is random matrix theory. It is used to describe phenomena in nuclear physics, mesoscopic quantum mechanics, and wave phenomena. Random matrix theory was invented in a bold attempt to describe the statistics of energy level spectra in nuclei. In many cases, the statistical behavior of systems exhibiting complex wave phenomena - almost any correlations involving eigenvalues and eigenvectors - can be quantitatively modeled using simple ensembles of matrices with completely random, uncorrelated entries!

This is an exercise that not only addresses fundamental issues of universality in spectra, but also is a simple introduction to generating random numbers, eigenvalues, and plotting.

Read directions and background in

• Random Matrix Theory Exercise.

All necessary files are linked at the left.